2023年12月26日来源:信管网 作者:cnitpm
信息系统项目管理师计算题考点:线性规划建模
考点分析:该考点经常考,需要大家掌握,只看理论是很难看懂的,需要大家多做题进行理解。
就其实质而言,线性规划问题是一类特殊的极值问题,它是在一定的线性约束条件下,追求某一个目标函数的最大值或最小值。线性规划问题的数学模型包含三个要素:决策变量、目标函数和约束条件。
线性规划问题:求线性目标函数在线性约束条件下的最大值或最小值的问题,通常称为线性规划问题。只含有两个变量的简单线性规划问题可用图解法来解决。
温馨提示:其实理论概念性的东西大家看看官方教程,了解下就可以了,重要的是怎么计算。
以下用一个例子为大家详细说明:
某企业需要采用甲、乙、丙三种原材料生产Ⅰ、Ⅱ两种产品。生产两种产品所需原材料数量、单位产品可获得利润以及企业现有原材料数如表所示:

则公司可以获得的最大利润是(1)万元。取得最大利润时,原材料(2)尚有剩余。
(2)
A.21
B.34
C.39
D.48
(2)
A.甲
B.乙
C.丙
D.乙和丙
【答案】B、A
解题步骤:
1、确定决策变量:根据影响所要达到目的的因素找到决策变量。一般为一个数量表示的量化方案或措施,即要确定的自变量。
本题说明了生产两种产品所需原材料数量、单位产品可获得利润以及企业现有原材料数,问的是最大利润及最大利润时的原材料数量,所以这个“变量”就是“产量(吨)”。我们设生产的产品I为x吨,产品II为y吨时,获得利润最大。
2、确定目标函数:由决策变量和所要达到目的之间的函数关系确定目标函数。
本题的目的是求利润最大,我们设为Smax,根据上述确定的变量及题目表格中的数据,确定目标函数公式为:Smax=9x+12y
3、确定约束条件:由决策变量所受的限制条件确定决策变量所要满足的约束条件。
本题的约束条件体现在原材料的供应有限量。因为生产产品I所需原材料甲为1吨,生产产品II也需要1吨,但现有原材料甲为4吨,所以:1x+1y≤4,即x+y≤4。
同理可得原材料乙的约束条件为:4x+3y≤12,原材料丙的约束条件为:x+3y≤6
根据以上3个要素,我们就可以得到线性规划问题的数学模型:
求x、y的值,使目标函数达到Smax=9x+12y,且满足约束条件:
x+y≤4
4x+3y≤12
x+3y≤6
4、求解
方法一:画图求解(需要掌握,画图的话简单直观,很容易得出答案)
这一步用文字很难让大家明白,大家可以去看一些视频讲解,简单来说就是:
(1)在平面直角坐标系xy轴上将上述约束条件不等式画出来
(2)然后画出目标函数等于0的直线:
(3)移动目标函数直线,求最大值时沿着矢量(目标函数增加)的方向移动;求最小值时沿着矢量(目标函数减少)的反方向移动;
(4)目标函数直线与可行域边缘相交的点的坐标就是最优解
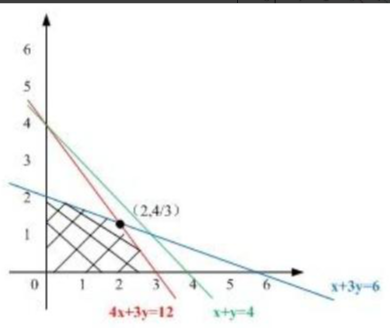
从上图可以很直观的看到,x=2,y=4/3时为最优解,有些考生可能会说,我能看到x=2,但y=4/3看不到啊!你随便代入一下那两条交叉线公式中的任意一条不就得到了吗,比如x+3y≤6,代入x=2,y≤4/3。
Smax=9x+12y=18+16=34
取得最大利润时,原材料甲使用:2+4/3
原材料乙使用:2×4+3×4/3=12
原材料丙使用:2+3×4/3=6
所以,取得最大利润时,原材料甲仍有剩余。
方法二:这题也可以直接组合不等式求解
这道题,我们先把:4x+3y≤12;x+3y≤6放一起求出x。很容易得到,x≤2,y≤4/3,然后代入x+y≤4,是符合该不等式的,所以得出该题答案,生产的产品I为2吨,产品II为4/3吨时,获得利润最大,即Smax=34。
有些考生可能会问为什么不是把x+y≤4,4x+3y≤12放一起求出x、y,然后代入x+3y≤6求解,当然可以,3个随意组合两个,然后代入另外一个都可以,不过最终需要代入之后不等式成立才可以。比如x+y≤4,4x+3y≤12放一起求出x、y分别为x≤0,y≤4,将结果代入x+3y≤6不成立。那么我就要换另外一组求解。
【真题演练】
某电池厂生产甲、乙两种型号产品(单位:万个),这两种产品都需要设备和A、B两种原材料,利润与资源限制条件如表所示,为了获得最大的利润,该电池厂每天生产的甲产品的数量应为( 1 )万个,此时该企业每天的利润为( 2 )万元。
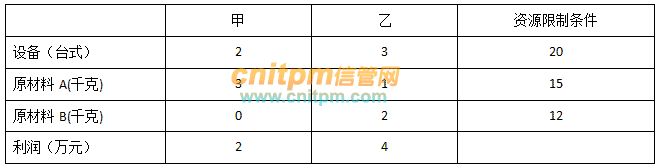
(1) A
A、1
B、2
C、3
D、4
(2)
A、20
B、22
C、24
D、26
查看答案
参考答案:A、D
温馨提示:因考试政策、内容不断变化与调整,信管网提供的以上信息仅供参考,如有异议,请考生以权威部门公布的内容为准!