信息系统项目管理师计算题考点：动态规划-资源分配问题

2024年01月16日来源：信管网作者:cnitpm

信息系统项目管理师计算题考点：动态规划-资源分配问题

温馨提示：一些概念性的东西大家首次看搞不懂的话不必过多纠结，直接看试题解析，当然文字描述的效果是赶不上视频讲解的，建议大家多看视频讲解。

有总数量为a的某种资源，用于生产n件产品，若分配数量x_i用于生产第i种产品的收益为g_i(x_i)，(i=1,2,…,n)，如何分配才能使总收益最大？

这种问题就是资源分配问题，准确来说是一维离散资源分配问题，因为信息系统项目管理师第4版官方教材上介绍的便是这种，所以一维连续资源分配问题、二维资源分配问题等就不介绍了，大家有兴趣的可以自己去查找相关资料看看。

该问题的数学模型可以表示为：

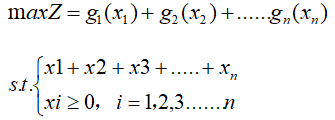
当收益函数g_i(x_i)均为线性函数时，该问题是一个线性规划问题，可以利用单纯形法进行求解；当收益函数为非线性函数时，问题变为一个非线性规划问题，如果我们采用非线性规划的方法求解将会非常麻烦。所以根据此类问题的特点，我们可以把它看成一个多阶段决策问题，利用动态规划的方法求解。

对于此类资源分配问题我们用动态规划的方法求解时，通常把资源分配给一个或几个使用者的过程作为一个阶段，将问题中的xi作为决策变量，将累计的量或随递推过程变化的量选为状态变量。

解题思路：

1、划分阶段k：通常把资源分配给一个或几个使用者的过程作为一个阶段，比如第1阶段就是资源分配给产品1，第二阶段就是分配给产品1和2，以此类推。

2、正确选择状态变量S_k：状态变量X_k可选择k阶段初所拥有的资源量，即X是要在第k项到第n项活动间分配的资源量

3、确定决策变量及允许决策集合：决策变量uk常常选对活动k的资源投放量，决策变量的允许集合是：0≤u_k≤X_k

4、确定状态转移方程：在选取上述状态变量和决策变量的情况下，状态转移方程是：X_k+1=X_k-u_k，取投放资源时的效益为指标函数，则g_k(u_k)为阶段效益指标

5、确定阶段指标函数和最优指标函数，建立动态规划基本方程：设f_k（x_k)为k阶段到n阶段按最优分配方案获得的最大收益，则动态规划基本方程是:

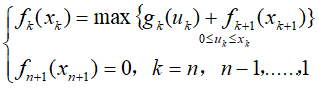
按基本方程，逆序计算，就可求得这类资源分配问题的最优解。

当然只看上面的内容，可能有很多考生是看不懂的，我们结合信息系统项目管理师第4版官方教材中的例子来说明下：

【例题讲解】某公司现有400万元用于投资甲、乙、丙三个项目，限制投资以百万元计，已知甲、乙、丙三项投资的可能方案及相应增加的收益如表所示，试确定使总收益最大的投资方案。

表项目投资收益值

(单位：万元)

项目	收益
项目	投资0万元	投资100万元	投资200万元	投资300万元	投资400万元
甲	0	300	600	1000	——
乙	0	500	1000	1200	——
丙	——	400	800	1100	1500

表中“—”表示不允许该项投资，即丙项目不能不投资，甲、乙项目都不能投资400万元。

【解析】

第一步：将对甲、乙、丙项目投资看作按顺序排列的3个阶段，即：甲（K=1）、乙（K=2）、丙（K=3）

第二步：确定状态变量SK：第K阶段初还剩余的投资额，比如K=1时，表示给甲投资之前还剩余的投资额，给甲投资之前也就是还没开始投资，当然就还剩400万。也可以说是第k阶段到第n阶段的总投资额。当K=1时，第1阶段到第3阶段，即给甲、乙、丙的投资总额为400万。

如果还不理解，再举个例子：

比如说给甲（第1阶段，K=1）投资了100万，这时候投资额还剩余400-100=300万元可以投资给乙和丙，也就是说在给乙投资之前（第2阶段K=2初，第1阶段K=2-1末）还剩300万（即：S2=300万元，也就是说给甲投资完后乙和丙的总投资额为300万元）。

第三步：确定决策变量及允许的决策集合：

决策变量X_k：对第K个项目的投资额。这个很好理解，比如给甲投资了100万，就是XK=100

允许的决策集合：0≤X_k≤S_K。这个就很好理解了，投出去的额度肯定要小于等于投之前还剩下的投资额，S₁=400，在给甲投资之前还剩下400万，总不可能给甲投资（XK）超过400万吧。

第四步：确定状态转移方程：S_k+1=S_K-X_k。搞清楚了前面几个概念，这个公式就很好理解了，比如给甲投资了100万，那么K=1时，即S₂（给甲投资了之后，准备给乙投资之前还剩余的总投资额）=给甲投资之前剩余的投资额（S₁）-给甲的投资额（X_K）=400-100=300。

第五步：确定阶段指标函数和最优指标函数，建立动态规划基本方程：

设阶段指标函数为：V_k(S_K，X_K)：X_k投资到第K个项目的收益。比如K=1时，V_K就表示投资到甲的收益。

最优指标函数f_k(S_k)：S_k投资到第K个项目至第n个项目时的最大收益。比如K=1时就表示投资甲、乙、丙的最大收益，也就是该题目的要求。

动态规划基本方程：

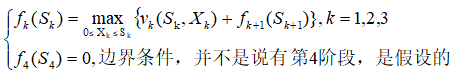
采用逆推法求解：

第一步：求第3阶段，K=3时，即给丙投资时收益最大值为：

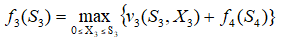
由f₄(S₄)到f₃(S₃)的递推过程：

根据题意S₃可能为400、300、200、100，S₃=X₃≠0。我可以得到下表：

S₃	X₃	V3(S₃,X₃)	f₄(S₄)	V₃(S₃,X₃)+f₄(S₄)	f₃(S₃)	*最优决策X^₃**
100万元	100万元	400万元	0元	400万元	400万元	100万元
200万元	200万元	800万元	0元	800万元	800万元	200万元
300万元	300万元	1100万元	0元	1100万元	1100万元	300万元
400万元	400万元	1500万元	0元	1500万元	1500万元	400万元

第二步：求第2阶段，K=2时，即给乙投资时收益最大值为：

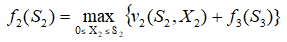
由f3(S3)到f2(S2)的递推过程：

根据题意S₂可能为400、300、200、100万元，X₂≠400，S₃=S₂-X₂≠0

S₂	X₂	S₃	V₂(S₂,X₂)	f₃(S₃)	V₂(S₂,X₂)+f₃(S₃)	f₂(S₂)	*最优决策X₂**
100万元	0万元	100万元	0元	400万元	400万元	400万元	0万元
200万元	0万元	200万元	0元	800万元	800万元	900万元	100万元
200万元	100万元	100万元	500万元	400万元	900万元	900万元	100万元
300万元	0万元	300万元	0元	1100万元	1100万元	1400万元	200万元
	100万元	200万元	500万元	800万元	1300万元
	200万元	100万元	1000万元	400万元	1400万元
400万元	0万元	400万元	0万元	1500万元	1500万元	1800万元	200万元
	100万元	300万元	500万元	1100万元	1600万元
	200万元	200万元	1000万元	800万元	1800万元
	300万元	100万元	1200万元	400万元	1600万元

第三步：求第1阶段，K=1时，即给甲投资时收益最大值为：

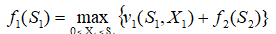
由f₂(S₂)到f₁(S₁)的递推过程：

根据题意S₁为400万元，X₁≠400，S₂=S₁-X₁≠0

S₁	X₁	S₂	V₁(S₁,X₁)	f₂(S₂)	V₁(S₁,X₁)+f₂(S₂)	f₁(S₁)	*最优决策X^₁**
400万元	0元	400万元	0元	1800万元	1800万元	1800万元	0元
	100万元	300万元	300万元	1400万元	1700万元
	200万元	200万元	600万元	900万元	1500万元
	300万元	100万元	1000万元	400万元	1400万元

至此我们就得出答案了:

当S₁=400万元时，最优决策得X^*₁=0元，于是S₂=S₁-X₁=400-0=400万元，从而查得最优决策X^*₂=200万元，所以X₃=400-200=200万元，所以给甲不投资，给乙投资200万元，给丙投资200万元时收益最大，收益为1800万元。

温馨提示：因考试政策、内容不断变化与调整，信管网提供的以上信息仅供参考，如有异议，请考生以权威部门公布的内容为准！

分享至：